5 Linear Algebra

A linear equation represents a line in n -dimensional space.

Definition 5.1 A linear equation has the canonical form

a_1⋅x_0+a_2⋅x_1+..+a_(n-1)⋅x_(n-1)=b.

 

where a_i and b are scalar constants and each x_i is a different variable.

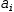
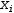
Myron has transformations that recognize expressions as linear equations. For recognition to succeed, the constants must be manifest scalar expressions. Anything else will take on the role of a variable. Also, the linear equation need not be in canonical form: y-3=2⋅x is recognizable as a linear equation.

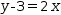
A linear system is represented in Myron by a tuple of linear equations suffixed with the ℓ pseudo-type operator (see §9.5.2).

A solution to a linear system is represented by a row vector. A manifest vector indicates a point solution. A vector of scalar expressions with variables indicates a set of solutions.

A set of solutions can be transformed into a linear surface (see §9.5.3). A linear surface is represented by a tuple of vectors suffixed with the L operator.

This section describes the Myron transformations that deal with linear systems, linear surfaces, matrix reduction and finding solutions to systems of linear equations.